Every summer, I participate in math photo challenge on Twitter. This week’s prompt was “area”; we were specifically instructed to “look for shapes made from one or more simple polygons or circles”. I found a very rich example right by the water fountain in the lobby of the San Diego Museum of Art.
I was particularly interested in how the upper semicircle was tiled. The specific area I’m talking about is shown in transparent white below.
There are lots of questions that can be asked here, and the one I settled on was
Express the area of the semi-disk in terms of the the area of the dark blue tiles.
In other words, if we were working with the large dark blue tiles, and we could cut them to fit the shape of the semi-disk and not waste any material (theoretically), how many blue tiles would we need? This would be a fun estimating question to ask of your student.
I eyeballed my picture of the tiles and realized that the radius of the semi-disk can be very simply expressed in terms of the diagonals of the light blue tiles.
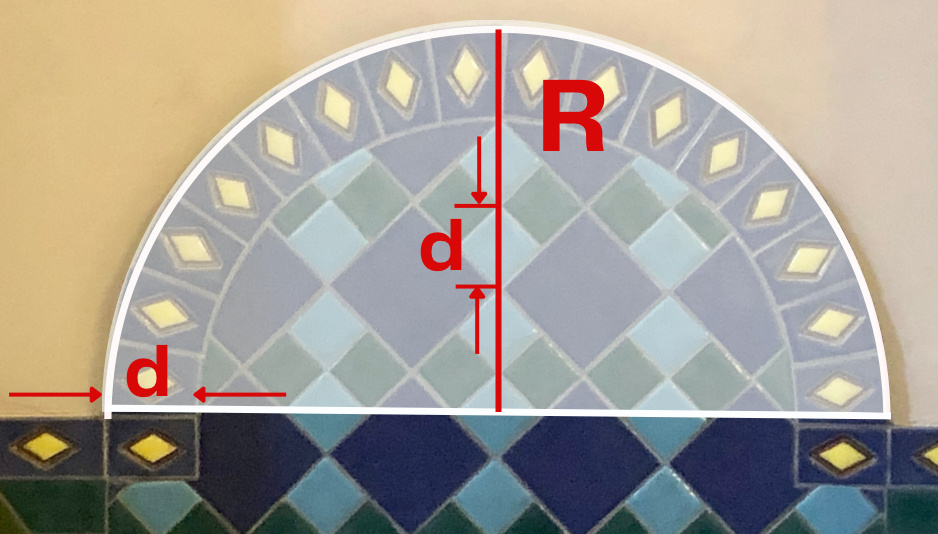
In the picture above, the radius of the semi-disk was denoted as R, and the diagonal of the light blue tiles is denoted as d. Note that the height of the outer band of the semi disks is equal d. Simply counting along the vertical radial line segment in the above diagram shows that R=4.5d. So the area of the semi-disk is
Now, the light blue tiles have area equal to 
:
The dark blue tiles have an area 4 times that of the light blue tiles, as you can see by comparing the squares outlined in red below:
So the dark blue squares have area equal to 
. To find out the area of the semi-disk in terms of the area of the blue tiles we divide the areas as follows:
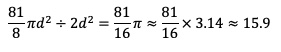
So the area of the semi-circle is roughly equal to the area of almost 16 blue tiles! Is that what you expected?
Ready for more? Find the area, in terms of blue tiles, of the inner semi-disk in the picture. That is, the semi-disk excluding the outer band of tiles with rhombi.