The world of tilings has recently had a breakthrough discovery: for the first time a single shape has been found that can cover the plane only in aperiodic patterns. That means that, unlike many patterns you see on wallpapers, buildings, or floors, the patterns created by these new tiles do NOT repeat themselves.
This is big enough news in the math world that it even made it into the New York Times! (See Siobhan Roberts’ Article “Elusive ‘Einstein Tile’ Solves a Longstanding Math Problem” on March 28, 2023.) People have been looking for this shape for quite some time now.
Sir Roger Penrose had been on a quest for years to come up with the smallest number of shapes to produce an aperiodic tiling, finally getting down to two shapes in what is known as the Penrose Tiling. The March 2023 paper “An Aperiodic Monotile” by Smith, Myers, Kaplan, and Goodman-Strauss shows that, in fact, just one shape is sufficient.
It turns out that “the hat”, as the shape is commonly called, can be made with the Geometiles 30-60-90 triangles:

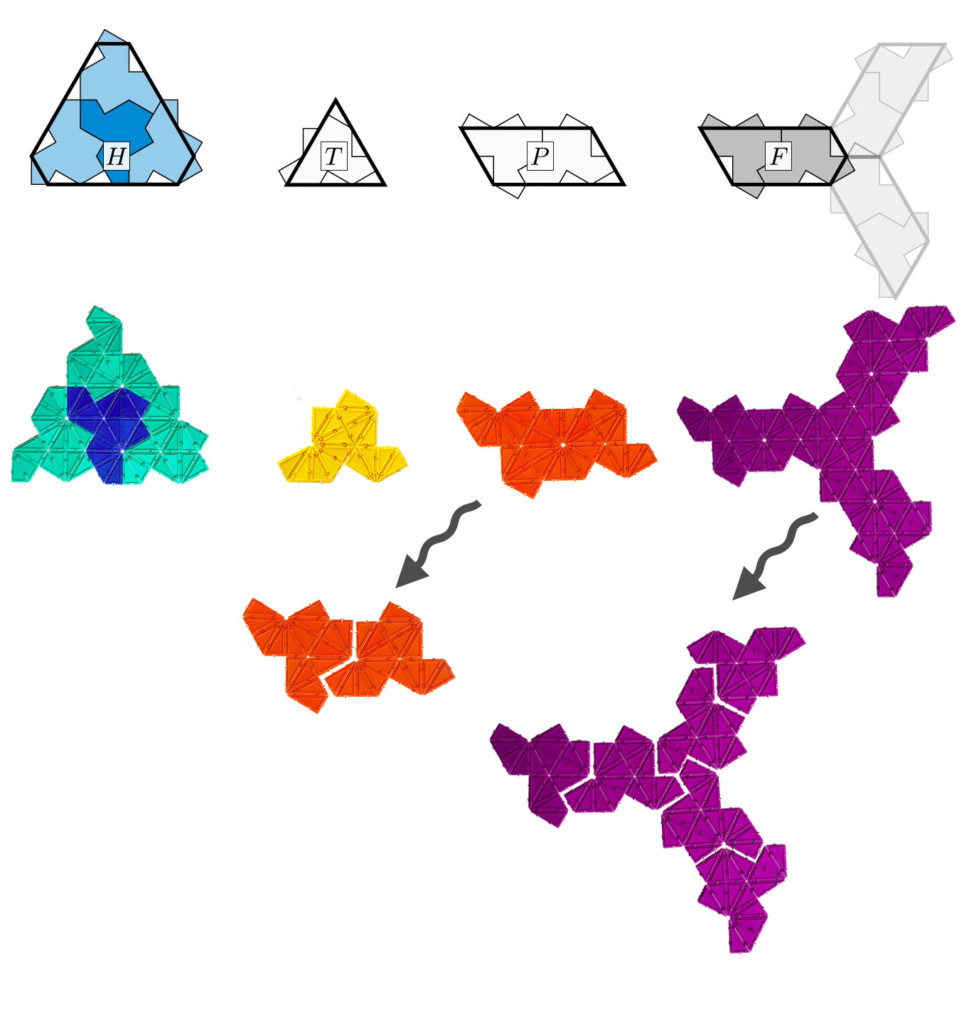
But it gets much more interesting. It turns out that these aperiodic tilings are made up of what the authors call metatiles. Each type of metatile is made up of one or more “hats”. And any aperiodic tiling with hats is built from metatiles, which fit together in prescribed ways. Here is an illustration from p.12 of the paper.
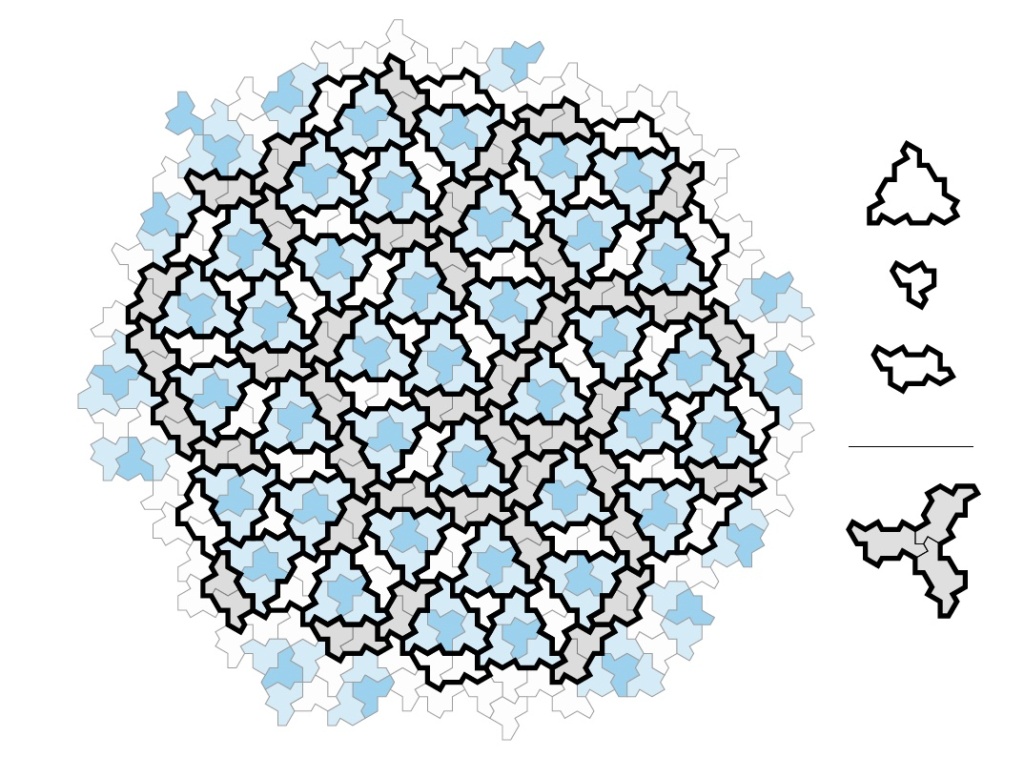
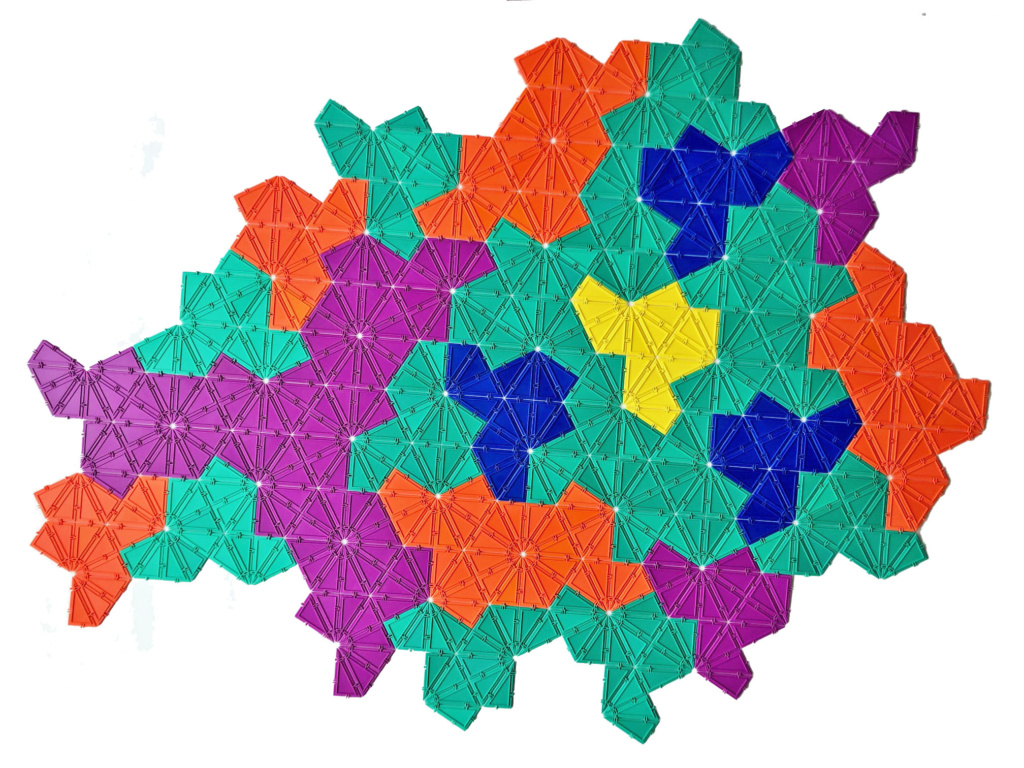
You can see from the above picture that the authors have chosen to color code the 4 types of metatiles in order to show they interlock to make the entire pattern. Below is a more detailed picture of the metatiles from the paper, together with the corresponding Geometiles models. The arrows point to the decomposition of the respective metatiles into hats.
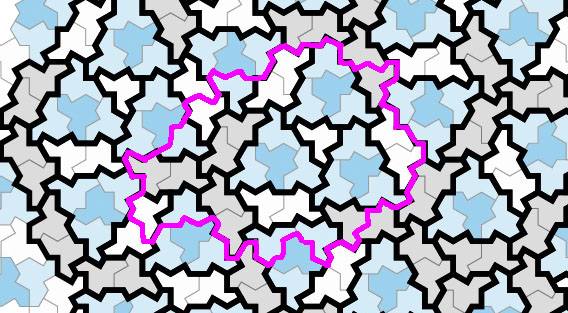
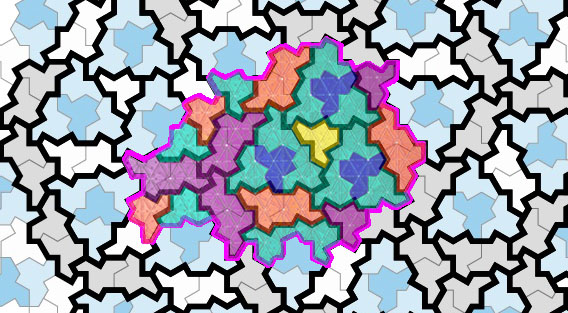
Armed with these metatiles, we can model any aperiodic tiling with hats. We finish by showing the modeling of the excerpt marked in pink below: