Delighting mathematicians, artists, and children alike, the Klein Bottle is a whimsical and perplexing surface that was discovered by the German mathematician Felix Klein in late 19th century. While it is most frequently seen visiting our three dimensional world in the form below,

its true home is 4 dimensional space; there it fits comfortably, without having to intersect itself. This is all beautifully described in the following video.
The Klein bottle is a classical example of an object studied by topologists. Topologists are mathematicians you may have heard described as not knowing the difference between a coffee cup and a donut. To put it roughly, topology is concerned with the essential characteristics of objects, and not so much with their precise dimensions. In other words, to a topologist, a coffee cup and a donut are the same object because the surface of one can be deformed into the other by stretching and pulling, but no ripping.
If you’re wondering what the essential characteristics of the Klein bottle are, most people would agree that being a non-orientable 2-dimensional smooth surface and having no boundary are among them. These properties can be well described from the point of view of an an imaginary ant crawling on a Klein bottle. The “2-dimensional smooth surface” part means that the ant would feel that any of its immediate neighborhoods appears to be just like a plane. “No boundary” means that there’s no edge from which it can fall. But the most distinctive feature is “non-orientable”.
Let’s back up for a second and talk about the simplest non-orientable surface— the Moeibus strip. You can make a Moebius strip easily at home by starting with a strip of paper, giving it half a twist, and taping it up, as shown below.

Have you ever seen M.C. Escher’s Ants print? There is an animated version of it that shows why the Moebius strip is non-orientable.
Let’s define orientation as the direction up from the ant’s head (since the ants are all going in the same direction, this is actually a mathematically sound way to define orientation on this surface). Suppose an ant is on a point on the surface, and the arrow pointing up from its head is the same as the direction up for the viewer. However, when it comes back to this same point later, it is crawling underneath, so the direction of the arrow from its head points down from the viewer’s point of view. In other words, we cannot consistently define orientation for any point on the Moebius strip, which is why we say it’s non-orientable. The Klein bottle has the same property of being non-orientable, since it’s made of two Moebius strips joined at their boundary (if you are curious how this works, it is illustrated here). With the recent addition of Mobies, Moebius strips can easily be built with Geometiles. So in theory, a Geometiles Klein Bottle should be possible. However, in practice the construction is fraught with challenges. This is due to the fact that our building materials consist of only a few types of polygons, and these polygons are almost rigid. It will turn out that “almost” is the operative word here.
Let’s have another look at the main image to have a better sense of these challenges.
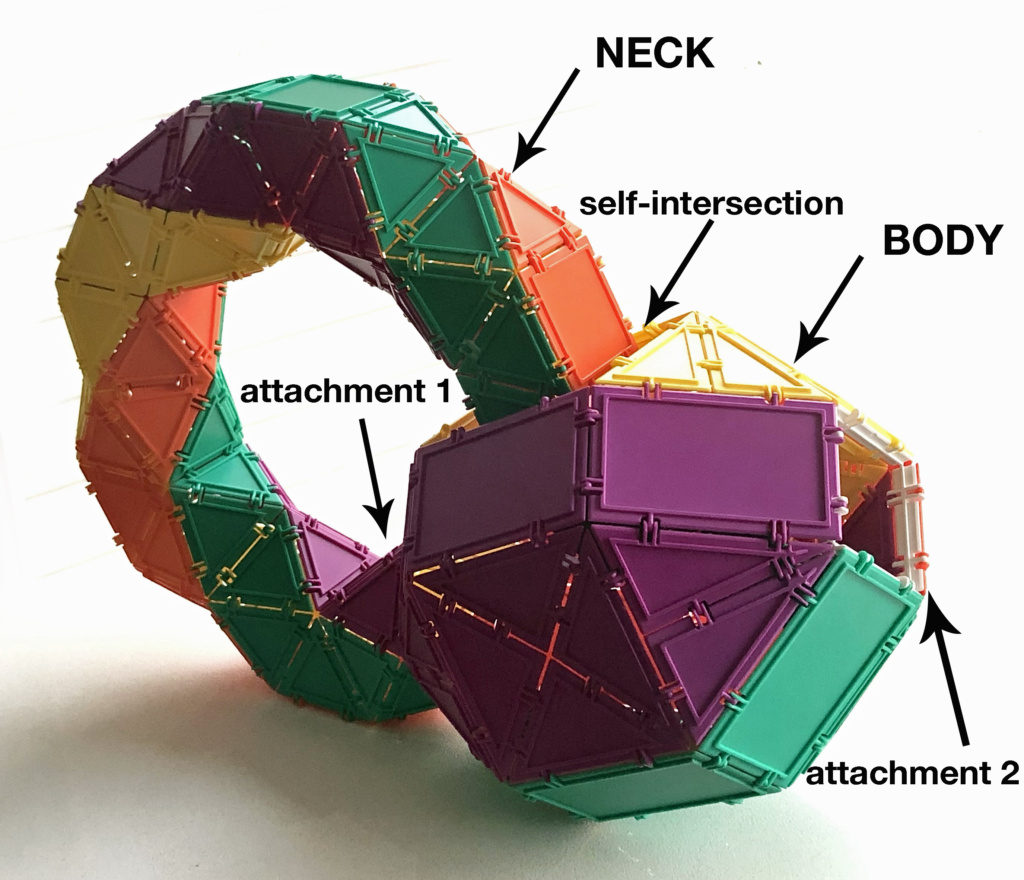
Due to my prior experiments with modeling of tori, I determined that the neck of the Klein bottle needs to be made mostly of square antiprisms. They allow for a graceful curve and lend themselves to a candy cane style coloration. In a Klein bottle, the neck is attached to the body in two places, as marked in the picture above. Both of those had to be square. In addition, the realization of the Klein bottle in 3 dimensions requires that the neck “intersects” the body as shown above. In order to model this with polygons, we need to have an opening in the polyhedral structure of the bottle body that is large enough to comfortably accommodate the bottle neck passing through it.
I decided that a modified rhombicuboctahedron shape would be a good candidate. This shape is very similar to a rhombicuboctahedron, but with golden rectangles replacing all but a pair of antipodal squares, and the non-antipodal squares being larger. So the neck can be attached at the two antipodal squares (see attachment 1, 2 above), and one of the larger squares can be knocked out to allow for the self-intersection.
Let’s pause here and have a look at the inside of the Klein bottle, with part of the body taken off to reveal the internal structure.

Constructing the shape of the neck so that it starts at the point of attachment 1 and ends up at the point of attachment 2 proved quite difficult. In fact, the fit is not perfect, but the slight flexibility of Geometiles allows it to snap into place. It is quite a nice 3D geometry exercise to find out exactly how much the ending of the neck near the attachment 2 deviates from the place of attachment.
The spiraling colors of the Klein bottle have a pedagogical as well as aesthetic reason. Imagine that you are an ant entering the Klein bottle from the Mobies sides, as shown in the figure below.

You are crawling on the yellow part, and as you travel inside the neck of the bottle and into the body of the bottle on the yellow, you always see purple to your left and orange to your right. However, when you come to the spot on the other side of where you started, and continue on the yellow path on what appears to be the outside of the bottle neck, you will find that purple is on the right and orange is on the left. This inconsistency in the orientation is exactly what makes for a NON-ORIENTABLE surface!
