Several years ago, I explored approximating Pi with polygons made of Geometiles. I described my findings in this blog. Fast forward to 2022, when Charles Fleischer showed me a polyhedral torus I’ve never seen before, and its boundary was a regular 30-sided polygon. The fancy name for a 30 sided polygon is triacontagon. Triaconta τριάκοντα (triaconta) means ’30’ in Greek, and γωνία (gōnía) means ‘corner’ or ‘angle’. I just had to get my measuring tape on this one! But first, I had to check if it was flat. Sometimes it’s hard to tell from a picture, especially one taken with a mobile phone camera.
What I was interested in is the interior angle of a regular 30-gon. It is the angle in the picture below:

The formula for this angle is derived here. It tells us that the interior angle of a regular n-gon is
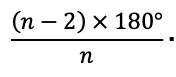
In our case, n = 30, so the interior angle is

Now, the regular pentagon has an interior angle of 108o, and the equilateral triangle has an interior angle of 60o. Adding them up we get 168o, which is exactly what we need to get a regular 30-gon! This is illustrated in the picture below.

We can finally determine how close to the value of π this 30 got gives us. Recall that π is the ratio of a circle’s circumference to its diameter. We measure the circumference of our 30-gon with a ribbon, and then measure the length of the ribbon, which turns out to be 73 inches long. The diameter is measured with a tape measure to be 23.125 inches.

So the approximation of π that we get from this torus is π≈73/23.125=3.16. Not bad at all!
You can build this structure and a myriad of others with a Geometiles Jumbo Set.
