A trip to the ladies room of the Arclight Cinemas in the local mall revealed a somewhat unusually shaped sink.

In case you’re wondering where the water drains, there’s a slit right along the back edge, shown by the blue arrow. But what happens if the drain backs up; how much water can a sink like this hold before it spills over? Let’s figure out its approximate volume.
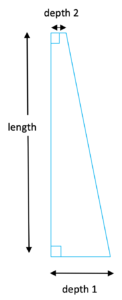
Before we start the calculations, let’s identify the shape of the sink. Recognizing the shape will help us get a better grip on the volume problem. The shape of the sink is a trapezoidal prism.

As with any prism, the volume equals the area of the cross section times the height. In our case, the cross section is a trapezoid. The area of a trapezoid is
(depth 1 + depth 2) x length.
Notice that this is the same as the area of a rectangle whose length is the same as that of the trapezoid and whose width half way between the two depths. You can see from the picture below that if we start out with a trapezoid, chop off the white triangle, and add an identical red triangle, we get a rectangle whose area is the same as that of the trapezoid.
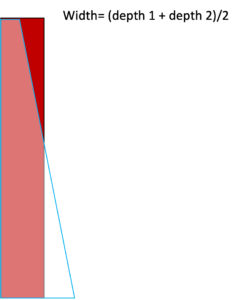
Back to our trapezoidal prism, we now see that its volume is:
½ (depth 1 + depth 2)× length × width
I had no measuring tape with me, so I just used whatever was immediately available to get a sense of the dimensions.

The width of the sink is about 2 1/3 lengths of the napkin, and the length is about a length of a napkin plus a width. The napkin was later measured to be 9 by 3 inches. So the width of the sink is about
2 1/3 × 9″ = 21″
while its width is about 9”+3”=12”. The smaller depth 1 looked to be about the same as the height of the display on my cell phone, which is about 4 inches, and depth 2 looked to be about an inch.
So the estimate for the volume of the sink is:
½(4″+1″)×12″×21″=630 in3.
There are 231 cubic inches in a gallon of water. So the volume of the sink is approximately
630/23 = 2.73 gallons.
The most common capacity for a bathroom sink is 3 gallons, so we know our answer is in the ballpark.
