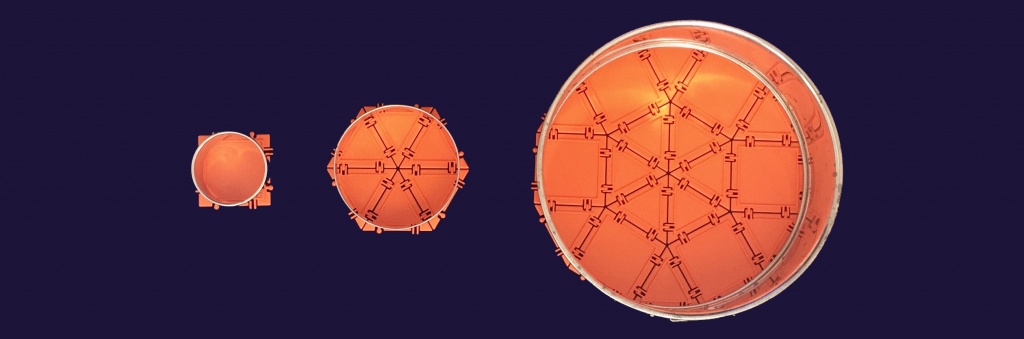
Nowadays, thanks to modern day computers, we have instant access to the approximation of π (the ratio of a circle’s circumference to its diameter) to any degree of accuracy. But back in antiquity, getting a good approximation of π was elusive and difficult. Over 2000 ago, the Greek mathematician and scientist Archimedes derived an accurate approximation of π using polygons to approximate a circle. Let’s follow in his footsteps with Geometiles as our tool.
We’ll start by approximating the circle with a square, then a regular hexagon, and finally a regular dodecagon (that’s a 12-sided polygon; dodeca means 12 in Greek). You can see that the more sides our regular polygon has, the rounder it is. In fact, the dodecagon is so round that it can almost roll like a wheel, as you can see in this Instagram video.
For each of our regular polygons, let’s compute the ratio of the circumference to the diameter of its inscribed circle, and see how it compares to π≈3.14.
What’s an inscribed circle, you might ask? That’s the largest round cookie you can make out of your polygon. Archimedes used both an inscribed circle and a circumscribed circle (the smallest circle that completely encloses the polygon) in his work on approximating π, but we’ll just stick to the former in this activity.
You can do this activity with your students at two levels.
For students who have not yet learned about special right triangles
Measure the sides of the polygons and the diameter of the cookie cutter, then compute the ratio of the first quantity to the second.
Let’s use the fact that the square is about 2.5 inches on the side. This is also the diameter of the inscribed circle. We are using the perimeter of the square to approximate the circumference of the circle. The perimeter of the square is 4×2.5=10 inches. So the ratio of the perimeter to the diameter is 10÷2.5= 4. This is our first approximation to π.

Let’s repeat with the hexagon. The side of each triangle is exactly the same length as that of the square: 2.5 inches. So the perimeter is 6×2.5=15 inches. The diameter of the circle is roughly 4.25 inches. The ratio of the perimeter to the diameter is 15÷4.25≈3.53.

Finally, the perimeter of the dodecagon is 12×2.5=30 inches and its diameter conveniently measures 9 inches (we knew that because we are using a standard 9 inch cake pan for this ;-)). 30÷9≈3.33

We can put our measurements in this table:

You can see the approximation getting closer to 3.14 as the number of sides grows from 4 to 12.
For students who are familiar with special right triangles
Use the properties of special triangles to compute the diameter of the circle in terms of the side length of one of the small squares.
Let the side of the small square be our unit 1. Then the perimeter of the hexagon is 6 units, and the then the diameter of the hexagon is √3. So the ratio of the perimeter to the diameter is 6/√3=2√3≈3.46. Not bad!
Now let’s see what happens when we use the dodecagon. The perimeter is 12 units. The diameter is √3+2. The ratio of the two quantities is 12/(√3+2)=-12(√3-2)≈3.22. Getting closer yet!
Archimedes continued this process with a 24 sided polygon and so on… not very practical for us, but by now, your students will have probably gotten into the spirit of Archimedes’ thought process. Happy Pi Day!