Among the myriad math lessons offered to us by the Olympic Games, here’s one involving just the rings. I recently challenged myself to model the rings using Geometiles, and came up with what you see against the background of the UCSD Track and Field Stadium. When Susan Lopez of LopezLandLearners saw this picture, she realized that it would make a great estimation problem: How many triangles and squares does it take to make one of these rings, just by looking at it? What a great way to start children thinking about estimates. We can also ask if there are more equilateral triangles or squares. As a next step, let’s have them count the shapes without driving themselves crazy. The underlined phrase refers to all those times when we lose track of where our starting point was, or someone distracts us and we have to start all over again. I made one separate ring so we can focus just on this task.
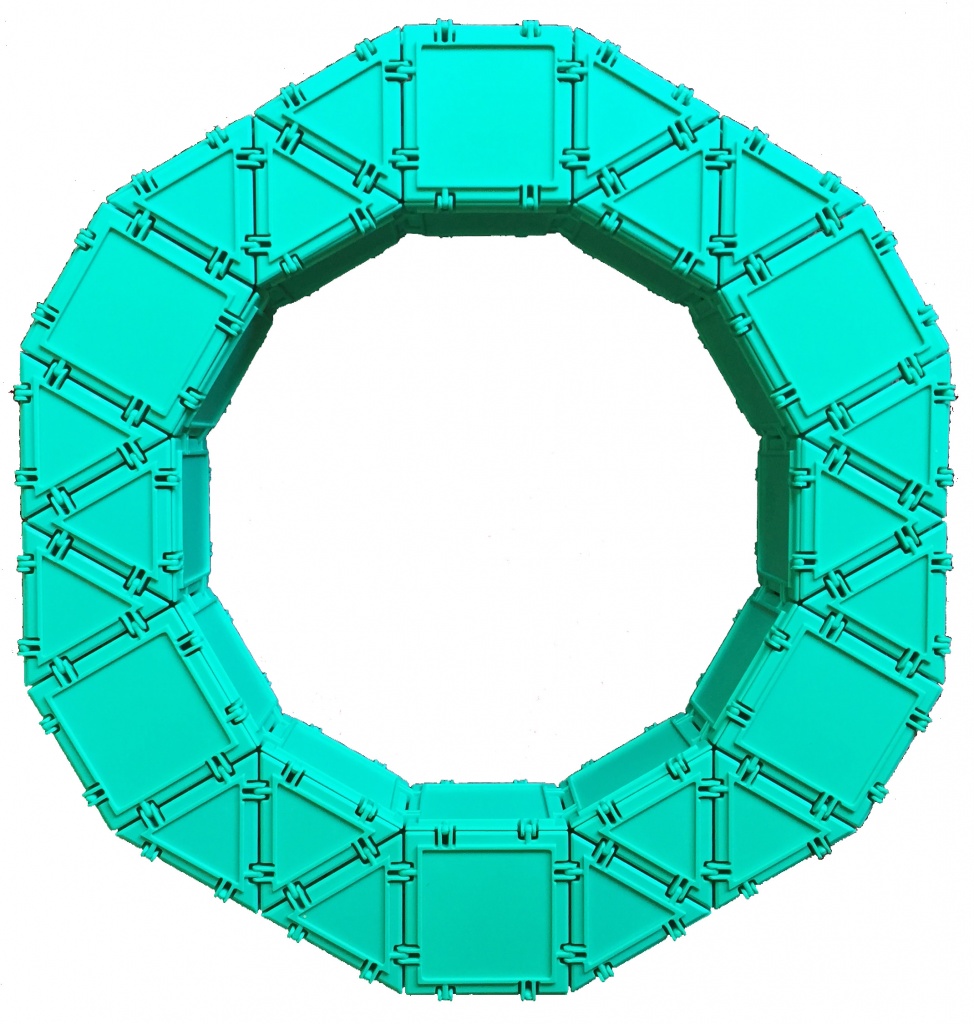
The bottom side of the ring looks exactly like its top side. Let’s start by noting the symmetries of the ring. There are 6 squares on the top side, and each two are separated by a triplet of equilateral triangles. So there are a total of 6 such triplets on top, resulting in 6 ×3=18 equilateral triangles. Since the bottom looks exactly like the top, there are a total of 18 ×2=36 equilateral triangles.
As for the squares, there are 6 on top and 6 on the bottom; the challenge is to count all the squares on the inside and the outside part of the ring. Those are the squares perpendicular to the top and bottom side. Let’s first focus on the number of squares in the inside part of the ring, outlined in purple:
The purple polygon drawn has 12 sides, and each side corresponds to a square. So there are 12 squares on the inside.
How many squares are on the outside of the ring? Those would be all the squares adjoining the orange polygon below.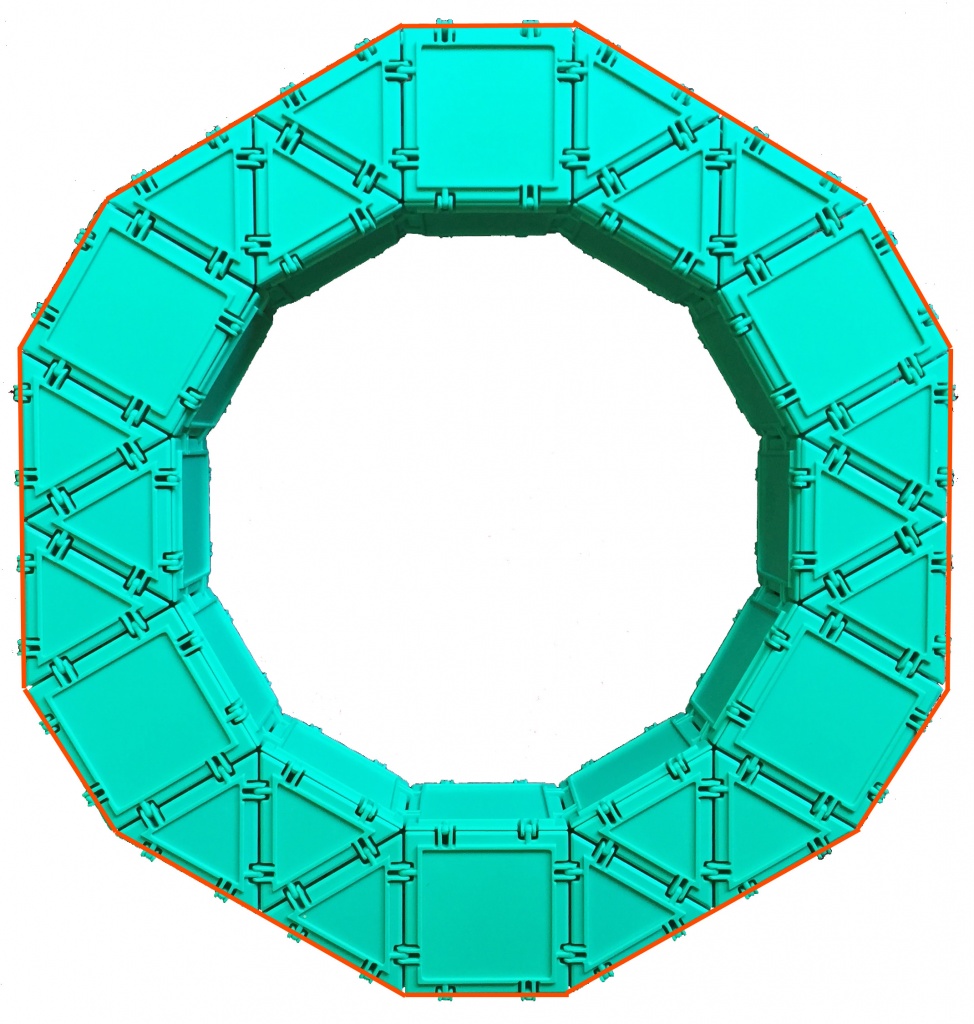
Let’s see exactly what the outside of the orange border looks like from the side.


We see that there is a square attached to each of the short orange sides and 2 squares attached to each of the long oranges sides. Since there are 6 short orange sides and 6 long orange sides, the total number of squares adjoining the orange 12-sided polygon is 6 + 6 × 2 = 18. Thus, the total number of squares in the ring is:
6 + 6 + 12 + 18 = 42
top bottom inner side (purple) outer side (orange)
We found that a single ring consists of 42 squares and 36 equilateral triangles.
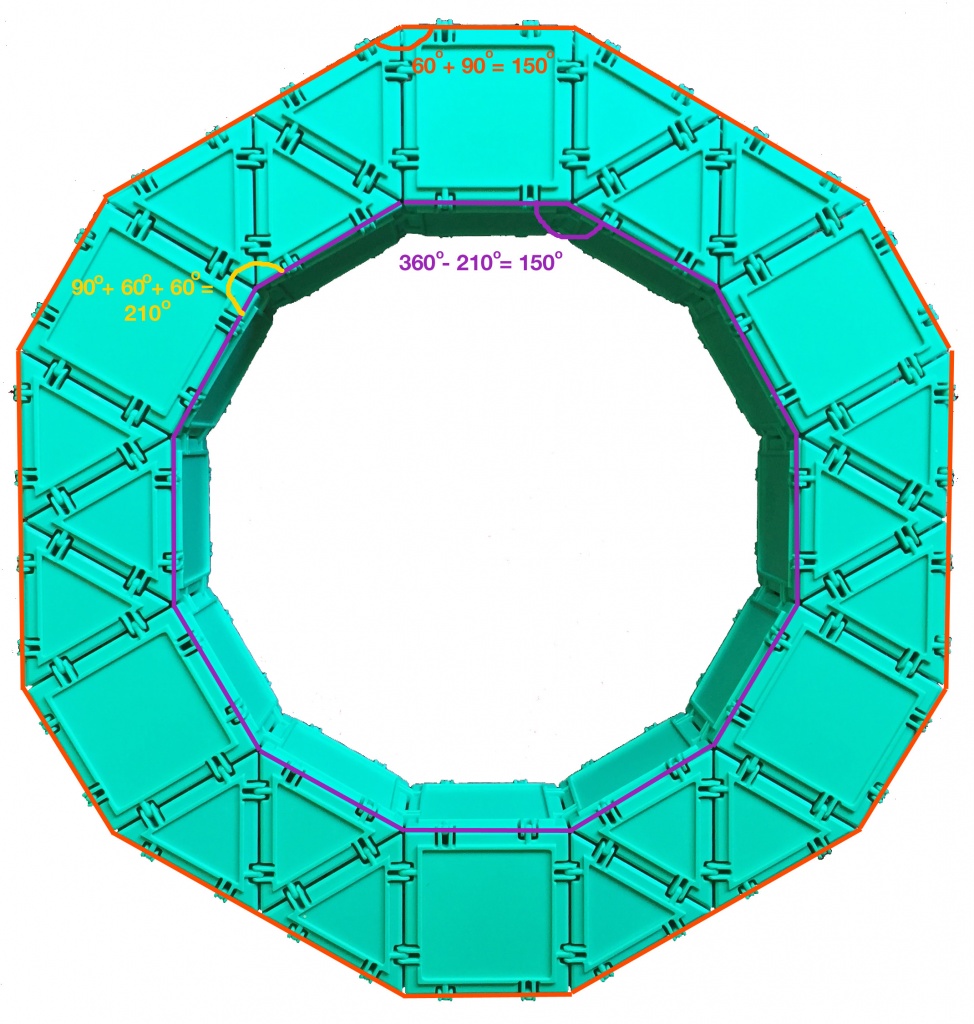
Note that in the process of counting, we came across an interesting fact about the outer (orange) and inner (purple) 12-sided polygons.
Both of them are equiangular (meaning the angles all measure the same), but only the purple one is also equilateral (meaning all the sides measure the same). In other words, the purple dodecagon (12-sided polygon; dodeca means 12 in Greek) is regular, but the orange one is not.
We can verify the angle measures as shown in the diagram below. This is a good exercise in reinforcing one of the 4th Common Core Standards for measuring angles, CCSS 4.MD.C.7, which says that students need to
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, e.g., by using an equation with a symbol for the unknown angle measure.