My friend from Spain recently invited me on a tour down mathematical memory lane. When she and her brother were in school, some time in the 1980’s, they made these geometric solids with their dad. Amazingly, their dad (who is now a granddad) kept the paper solids for all these years and recently gave them to my friend.

I’ve always been curious about what different cultures find mathematically significant, so I was very eager to see the geometric solids. You can see how delightful the paper models are in the picture above. Notice the altitudes drawn on the faces of the tetrahedron, along with the markings for the right angles.
What’s most important is that my friend has positive memories of learning math due to her father’s thorough hands-on teaching methods, and is now teaching her own children math.
The models were starting to come apart at the seams after more than 20 years, and I could see that they were made from nets similar to this one:
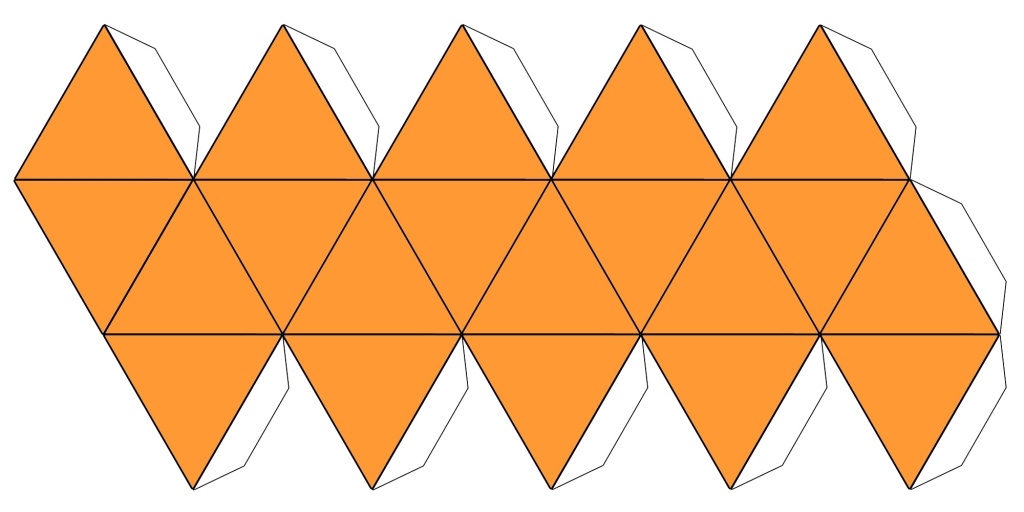
I thought it might be fun to ask my friend’s 9 year old daughter to reconstruct some of these solids with Geometiles. We started with the hexagonal prism and then moved on to the icosahedron. You can see the girl examining her mom’s assembled paper solids in the pictures at the top. As I watched the incoming 4th grader figure out how to make the paper models, I realized what an excellent starting point the paper models made. They gave us a tangible prompt for discussing the attributes of the shapes. For example, in the case of the icosahedron, one has to decide what shapes are needed for the faces, and how they are connected together.
Then a simple observation occurred to me: in the paper net, the triangles are already pre-assembled together. One need not necessarily make the observation that there are 5 triangles meeting at every vertex. This is a salient characteristic of the icosahedron; moreover, counting the number of polygons meeting at a vertex is a fundamental principle in the study of 3D geometry. However, in the paper net one simply has to fold along the creases and glue the tabs. When constructing an icosahedron out of Geometiles or any other construction set, one has to make a very deliberate choice of assembling 5 triangles at every vertex and applying this principle to every vertex until the figure is completed. This makes for a much more challenging and active learning scenario than using paper nets. Alternatively, you can construct your own net out of Geometiles, and then assemble it into an icosahedron.
Any way you do this, the paper models are an inexpensive and accessible starting point for the study of polyhedra. But to delve deeply into the subject, one needs to construct these polyhedra from completely unassembled parts.
