This year’s Nobel Prize in physics brought into the limelight the subject of topology, which studies the property of figures that remain unchanged under stretching and twisting, as long as there is no tearing. As a member of the Nobel Prize committee explained in this article, a topologist is concerned with distinguishing a Swedish pretzel from a bagel not due to their taste differences, but due to the fact that a pretzel has two holes and a bagel has one. To a topologist, the pretzel is a surface of genus 2, and a bagel is a surface of genus 1, where the genus number simply corresponds to a number of holes.
What would you say if a topologist told you that this cubical framework is a surface of genus 5? Meaning that if you stretched it out, it would look just like a bagel with 5 holes.
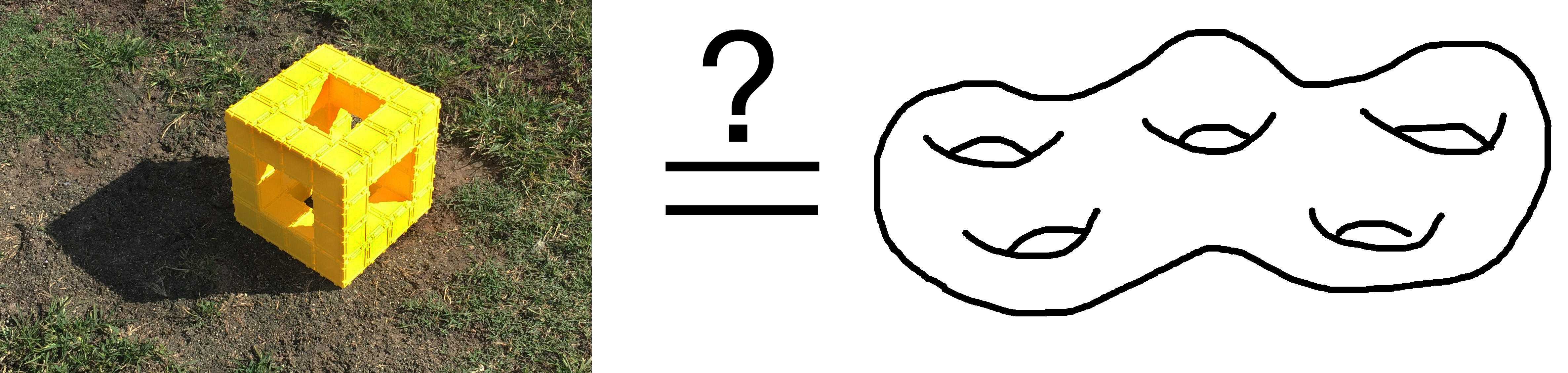
If your reaction is “Whoa!”, you wouldn’t be alone. Luckily, from the point of view of a 360 camera placed inside the cubical frame, the topologist’s claim no longer seems that unreasonable.
Have a look at this:

The large picture was taken with a 360 camera placed in the middle of the cubical frame, inside the green square. You can actually see the camera in the picture in the upper right. The colored lines in the different pictures show the same parts of the structure. You can see that the purple opening is distorted by the 360 camera to a quatrefoil shape. The distorted view allows you to see what would happen if you stretched the opening bound by the purple line so much that it becomes the outside boundary of the bagel. Looking at the large picture, you can clearly see the 5 holes of the “bagel”: one int he middle where the camera is, and four around it. Now, that’s a BAGEL!
